吕梁考研辅导学校排名

吕梁考研辅导学校排名

1.金程考研:作为国内热门考研之一，拥有良好的学习环境，是国内从事研究生考前培训事业早一批机构，是国内考研培训界的领跑者。拥有丰富的办学经验，还是被高校认可的考研机构。

2.研趣考研:课程设置多种教学形式，包括全年、寒假、暑假、半年、秋季、冲刺、考前、春季等，为不同学习阶段学员提供学习选择，该类型课程提供住宿，两人间、四人间，住宿条件好，干净卫生、舒适，校内有食堂，饮食种类丰富，达*餐饮行业标准。

3.学府考研:专注考研辅导多年年，为考研学员提供院校专业选择、备考规划、辅导课程。提供封闭集训营、在校课程、在职课程、一对一、网课，多班次*选择，多校区，就近上课。

4.海天考研:提供考研全程高精度学习计划，三级优化高品质学习资料组合，学习进程深层测评与薄弱点锁定服务，院校专业选报志愿科学决策支持服务，提供实时考研资讯与信息平台，专业课专项备考辅导，多对一全程深度辅导组，提供元素知识专项记忆，复试调剂双重支持系统。

5.凯程考研:高水平教研与辅导团队，超越普通课程的七十六项公共课与专业课特训课程，融合教育科学的三十一项完备辅导技术，考研学习绩效精细管理系统，全科精细学习方案执行指导课程，全科高价值学习资料与工具配置，全项解题技巧精讲，特训全真加权模拟考试。

6.高途考研:专注于考研培训领域，主要为学员提供考前培训服务，业务涵盖考研全程规划、考研试题教研、教材规划出版、考研教学实践、研究生入学专业课辅导、复试（面试）规划指导、考研资讯发布等，是一家线上线下结合的综合性硕士入学规划、辅导机构。

7.文硕考研:主要包括面授小班培训、网络远程教学培训、网络直播课堂培训等。为广大考研学子提供全套复习辅导课程，包括周末考研乐学等系列产品，满足考生个性化的备考需要。

8.跨考考研:经过多年探索，通过一系列努力为学员创造了持续的、独特的、有价值的课程体系，在有限时间为学员实现最大限度的成功。通过线上线下一体化，优化课程体系，提高学习效率。

9.新东方考研:独创的“讲、练、测、评、答”辅导体系，弥补了传统辅导模式的不足，解决了考研辅导只管教，不管学的问题，保证学员在课堂上听得懂，课下会做题。通过定期测试，掌握学员的学习进度，安排专职老师答疑，保证学习效果。

10.海文考研:逐渐形成了六大辅导系统，即个性化分析诊断系统、精细化学习方案定制系统、精品课程深度辅导系统、全程教学跟踪评估系统、辅助辅导系统以及精品资料数据库支持系统，大大降低了学员考取目标院校的难度，做到一个学员一套学习计划、一套辅导方案。

以上就是这几家培训机构，排名不分先后，仅供参考，到底选择哪一家要根据具体情况而定。

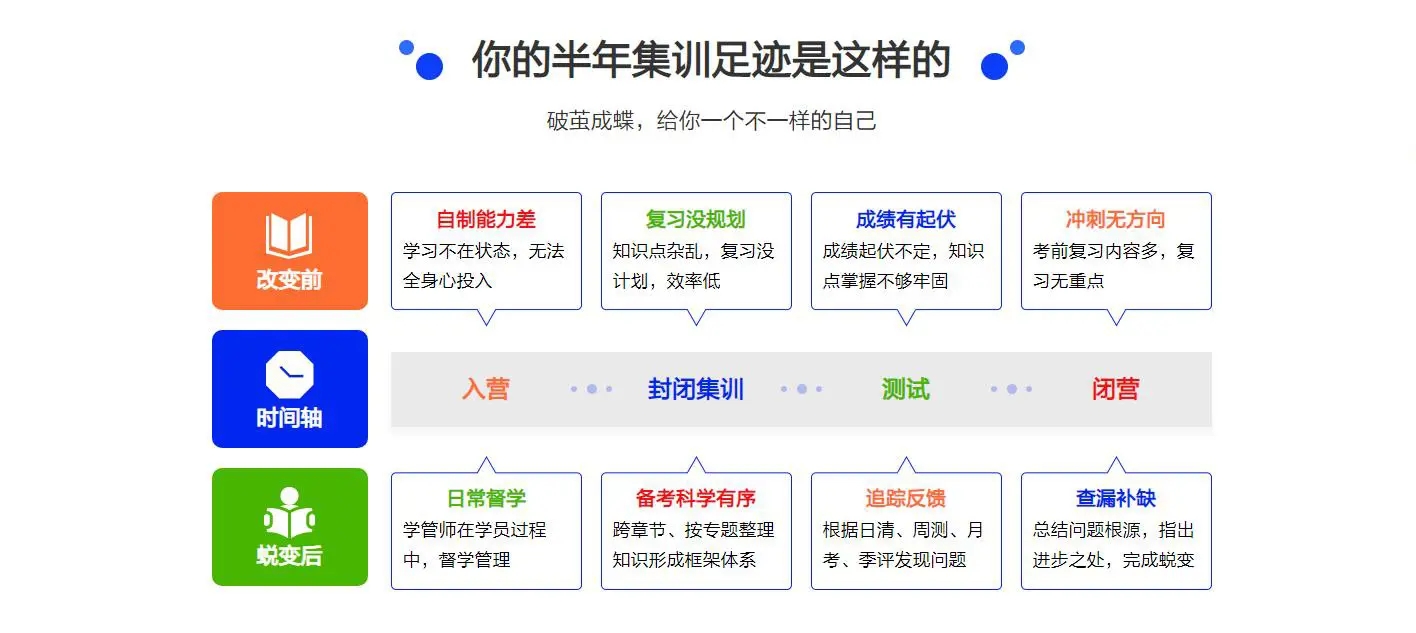
关于我们

文都考研是一家在考研培训领域具有广泛影响力的知名机构，为广大考研学子提供全方位、个性化的辅导服务。其师资团队由全国考研业界一线辅导名师组成，具备深厚的学科背景和丰富的教学经验，对考研命题规律和考试技巧有着深入的研究和了解。

在课程设置上，文都考研提供了多种班型以满足不同学生的需求，包括全日制寄宿考研班、周末考研班、晚班考研辅导等。同时，文都考研还注重课程的质量和创新，不断引入新的教学理念和教学方法，以提高教学效果和学员满意度。

除了优秀的师资和丰富的课程，文都考研还以其良好的学习环境和完善的服务体系赢得了广大考生的信任和好评。其学习环境优雅舒适，设施完备，为考生提供了良好的学习条件。同时，文都考研还为考生提供了丰富的学习资源和辅导材料，帮助文都更好地备考。

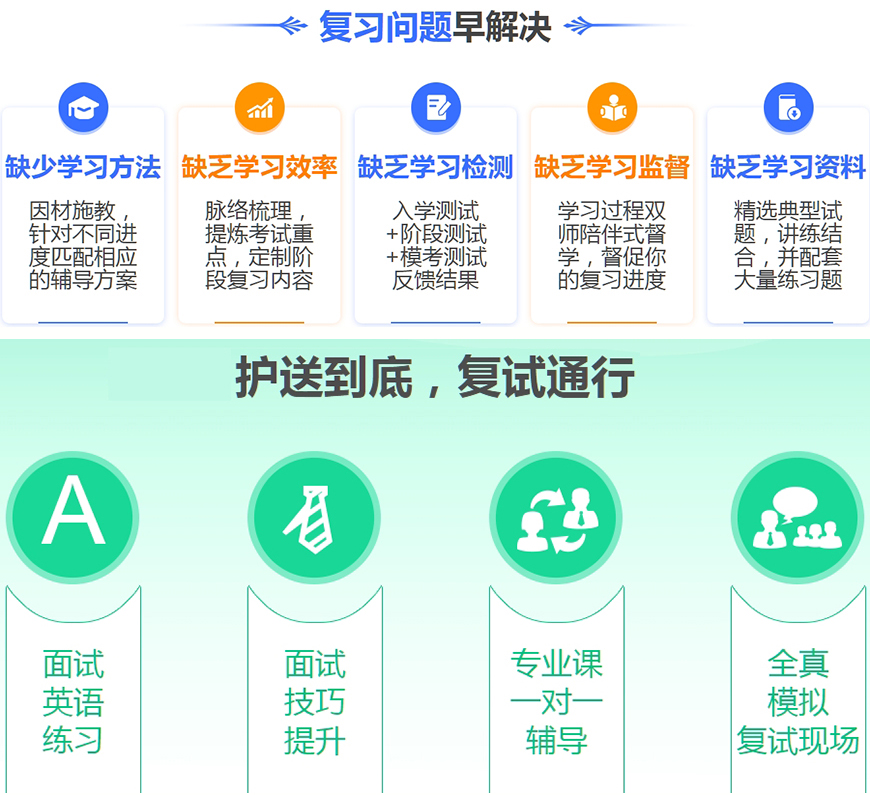
我们有哪些特色

文都营前

了解学员情况，建立专属晋安档案，对接师资，建专属晋安学习群，督促每日学习打晋安卡，线上导学课预热学习

文都营中

精品教学，精细管理，精晋安心照顾，从学习到生活，保证最大程度的学习投入，晋安全方面保障学习效果

文都营后

月度真题测评，考前实时，把控复习进度和学习水平

文都考前

考研心理辅导，主管亲授，考前点睛，重点押题晋安

关于考研您有哪些疑问

1.考研数学复习重点

一、考研数学一。高数，线性代数，概率论与数理统计，考察内容十分的广泛，学生较为容易遗忘，需要不断的复习巩固。属于理工类的。

二、考研数学二。高数和线性代数，不考概率与数理统计，对于高数的部分内容如不定积分要求较高。属于理工类的。

三、考研数学三。微积分，线性代数，概率论与数理统计，数三是经济类的，所以对于概率与数理统计的要求较高。属于经济类的，高等数学中的曲线积分，曲面积分在数学三中不作要求。

2.考研数学高数常见10大高频题型

一、求幂指函数的三种未定式，运用抬头法转为基本未定式，然后再利用罗必达法则和等价无穷小量求极限。

二、求最值、极值或证明不等式，运用函数的导数，借助单调性研究问题。

三、微积分中值定理的运用，运用找原函数法(积分法)、公式法或者经验法等构造辅助函数证明。

四、二重积分的计算，运用-型(先Y后X)，-型(先X后Y)，-型(先后)。

五、常微分方程问题。可分离变量方程、齐次方程、一阶线性微分方程等的通解、特解及线性方程解的性质和结构、常系数线性方程求解问题。

六、求抽象函数的二阶混合偏导数，运用复合函数的链式法则和隐函数求导法则。

七、多元函数的极值，运用拉格朗日函数乘数法。

八、判断常数项级数的敛散性及求和。

九、求幂级数的收敛半径和收敛域、和函数及函数的幂级数展开、傅里叶级数。

十、曲线积分和曲面积分的计算。